physics help....
Replies
-
seriously...
your name = so faking rad....
i thought it was sofa king rad....
bahahahahahahaha
It's sofa king rad.0 -
there isnt a picture to post... i could like draw it out and kinda show you what i THINK it is asking... or do you need a picture of the force table???
No, I don't need a picture of hte force table now. I think I know what it's asking. I think it's in Quadrant 3, just intuitively because the two forces that you know are there are in Quadrant 1. Equal and opposite reaction shows that the opposit reaction would be roughly in quadrant 3. But, you need to prove that.
SEE I WAS RIGHT!!!!! YAY FOR ME!!!!!
I bet you never thought a homeless hobo who smells of booze and cigarettes would discuss physics with you, huh?
we are on the same brain wave! LOL! If you weren't homeless, I would come over right now!
I'm not technically homeless. My local park is my home.
Can you get to pan handling for spare change so you can buy me a drink! I will be there in a bit!
I already have my booze here. I keep it on me at all times since I'm an alcoholic.
Ok, I am on my way. Don't drink all the booze!0 -
Actually, you can only prove that mathematically if you know the magnitude of the forces. So, my answer would be the third quadrant, Only becaus the two applied forces are in the first quadrant, your reactive force would be in the third.
I agree with this answer if the applied forces are PULLING away from the force balance at 20 and 80 degrees. The reaction force would have to be pulling back at some angle in Q3. I think that's a reasonable assumption to make even though it just says the forces are "applied" at those angles, so really it could be a pulling or pushing force (if pushing at those angles the answer would be Q1). But remembering way back to textbook type questions are written Q3 is the most likely answer.
Even if the forces were flipped in such that they are pushing the ring, the reactive force would sitll be in quadrant 3 since the resultant of the two forces are within quadrant one.
Stll right with answer C.!0 -
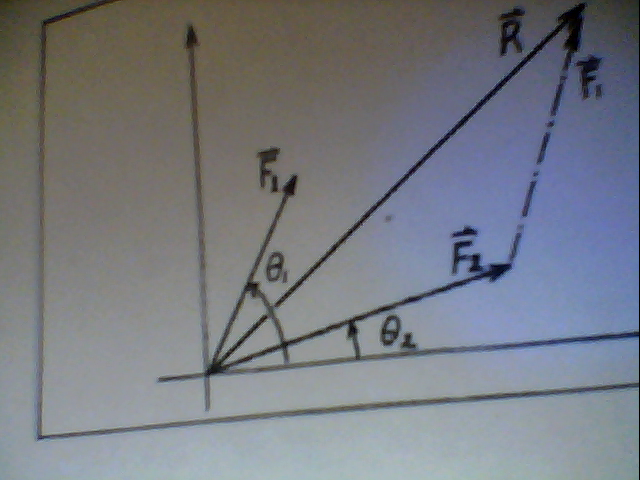
Question:
Two forces are applied to a ring of a force table, one at an angle of 20 degrees, and the other at an angle of 80 degrees. Regardless of the magnitudes of the forces, will the equilibrant be in the
A) first quadrant second quadrant
second quadrant
C) Third Quadrant
D) Fourth Quadrant
E) You cannot tell which quadrant from the available information....
You're over thinking this. 20 degrees and 80 degrees are both in the first quadrant (0 to 90 degrees). Two vectors in the first quadrant are going to have a sum vector also in the first quadrant.
So the question is: "If you have two forces in the first quadrant, in what quadrant do you need to apply an opposing force to balance the sum of those two?"
The balancing force has to be 180 degrees from the vector sum of the two forces. Since the vector sum is in the first quadrant (somewhere between 0 and 90 degrees), the balancing force has to be in the third quadrant (somewhere between 180 and 270 degrees).0 -
there isnt a picture to post... i could like draw it out and kinda show you what i THINK it is asking... or do you need a picture of the force table???
No, I don't need a picture of hte force table now. I think I know what it's asking. I think it's in Quadrant 3, just intuitively because the two forces that you know are there are in Quadrant 1. Equal and opposite reaction shows that the opposit reaction would be roughly in quadrant 3. But, you need to prove that.
But for a force table, the forces pull "out", not "in". Hence, they pull away from the point of intersect.
since both forces are in the 1st quadrant, their resultant vector is going to be somewhere between 20 deg and 80 deg.
The equilibriant force (3rd) force is going to be pulling in the same line as that combined vector, but in the negative (opposite) direction. So it'll be in the 3rd quarter.0 -
Question:
Two forces are applied to a ring of a force table, one at an angle of 20 degrees, and the other at an angle of 80 degrees. Regardless of the magnitudes of the forces, will the equilibrant be in the
A) first quadrant second quadrant
second quadrant
C) Third Quadrant
D) Fourth Quadrant
E) You cannot tell which quadrant from the available information....
You're over thinking this. 20 degrees and 80 degrees are both in the first quadrant (0 to 90 degrees). Two vectors in the first quadrant are going to have a sum vector also in the first quadrant.
So the question is: "If you have two forces in the first quadrant, in what quadrant do you need to apply an opposing force to balance the sum of those two?"
The balancing force has to be 180 degrees from the vector sum of the two forces. Since the vector sum is in the first quadrant (somewhere between 0 and 90 degrees), the balancing force has to be in the third quadrant (somewhere between 180 and 270 degrees).
This guy gets it.0 -
there isnt a picture to post... i could like draw it out and kinda show you what i THINK it is asking... or do you need a picture of the force table???
No, I don't need a picture of hte force table now. I think I know what it's asking. I think it's in Quadrant 3, just intuitively because the two forces that you know are there are in Quadrant 1. Equal and opposite reaction shows that the opposit reaction would be roughly in quadrant 3. But, you need to prove that.
But for a force table, the forces pull "out", not "in". Hence, they pull away from the point of intersect.
since both forces are in the 1st quadrant, the resultant equilibrium is also in the 1st quadrant.
The equilibrium is somewhere in between 20 and 80 degrees.
Doesn't matter if they are pushing or pulling. The reactive force to keep it in equilibrium is 180 degrees from the resultant of the two known forces, which puts it in the third quadrant.0 -
Kinda like that band named Sofa Kingdom.seriously...
your name = so faking rad....
i thought it was sofa king rad....
bahahahahahahaha
It's sofa king rad.0 -
yeah, mis-read the Q. i was thinking resultant of just the two vectors, not the 3rd equilibriant.0
-
there isnt a picture to post... i could like draw it out and kinda show you what i THINK it is asking... or do you need a picture of the force table???
No, I don't need a picture of hte force table now. I think I know what it's asking. I think it's in Quadrant 3, just intuitively because the two forces that you know are there are in Quadrant 1. Equal and opposite reaction shows that the opposit reaction would be roughly in quadrant 3. But, you need to prove that.
But for a force table, the forces pull "out", not "in". Hence, they pull away from the point of intersect.
since both forces are in the 1st quadrant, the resultant equilibrium is also in the 1st quadrant.
The equilibrium is somewhere in between 20 and 80 degrees.
Doesn't matter if they are pushing or pulling. The reactive force to keep it in equilibrium is 180 degrees from the resultant of the two known forces, which puts it in the third quadrant.
Agreed. If the first two forces are pulling, the answer would only be the first quadrant if the third force was for some unexplained reason pushing. And vice versa is the first two are pushing.
I have a BS in Physics and have never heard of a "force table." From the net:A force board (or force table) is a common physics lab apparatus that has three (or more) chains or cables attached to a center ring. The chains or cables exert forces upon the center ring in three different directions. Typically the experimenter adjusts the direction of the three forces, makes measurements of the amount of force in each direction, and determines the vector sum of three forces. Forces perpendicular to the plane of the force board are typically ignored in the analysis.
Cables or chains can't push. They only pull. So the regardless of the magnitude of any of the forces, the third (equalibriant) force must pull in the third quadrant since the vector sum of the first two pulls in the first quadrant.0 -
there isnt a picture to post... i could like draw it out and kinda show you what i THINK it is asking... or do you need a picture of the force table???
No, I don't need a picture of hte force table now. I think I know what it's asking. I think it's in Quadrant 3, just intuitively because the two forces that you know are there are in Quadrant 1. Equal and opposite reaction shows that the opposit reaction would be roughly in quadrant 3. But, you need to prove that.
But for a force table, the forces pull "out", not "in". Hence, they pull away from the point of intersect.
since both forces are in the 1st quadrant, the resultant equilibrium is also in the 1st quadrant.
The equilibrium is somewhere in between 20 and 80 degrees.
Doesn't matter if they are pushing or pulling. The reactive force to keep it in equilibrium is 180 degrees from the resultant of the two known forces, which puts it in the third quadrant.
Agreed. If the first two forces are pulling, the answer would only be the first quadrant if the third force was for some unexplained reason pushing. And vice versa is the first two are pushing.
I have a BS in Physics and have never heard of a "force table." From the net:A force board (or force table) is a common physics lab apparatus that has three (or more) chains or cables attached to a center ring. The chains or cables exert forces upon the center ring in three different directions. Typically the experimenter adjusts the direction of the three forces, makes measurements of the amount of force in each direction, and determines the vector sum of three forces. Forces perpendicular to the plane of the force board are typically ignored in the analysis.
Cables or chains can't push. They only pull. So the regardless of the magnitude of any of the forces, the third (equalibriant) force must pull in the third quadrant since the vector sum of the first two pulls in the first quadrant.
I never heard of one either. I googled it. I wasn't talking about the force table itself, I was just saying that regardless if you could push or pull on it, it's still third quadrant for a resultant if it is in equilibrium.0 -
use this animation - hopefully helps: http://www.mrwaynesclass.com/teacher/Vectors/Force_Table/0
-
I never heard of one either. I googled it. I wasn't talking about the force table itself, I was just saying that regardless if you could push or pull on it, it's still third quadrant for a resultant if it is in equilibrium.
Right. The sign of the third force would have to be the opposite of the first two forces for some reason not explained by the problem.
In any case, Index has explained why he was saying first quadrant instead of third. He thought the question was which quadrant will the sum be in, not which quadrant the equalibrant will be in.
For what it's worth, I'd never heard the word equalibrant before today either!0 -
Imagine my suprise to see this post was actually what the topic was about.0
-
my biggest issue is like how to find force? do i automatically multiply is by 10? and if so why? I mean force= mass*acceleration, but i dont know the mass, so does that mean i cant figure it out?!
I'm not a physics major, but my initial thought was E when reading your question. Hope you find your answer soon. :flowerforyou:0 -
If anyone has any questions about long division, I'm here.0
-
Can someone please go on the record and say that my answer was just as correct as the ones with the fancy explainations! I mean, why can't a girl get props when she was the first one with the correct answer! just sayin'!0
-
Can someone please go on the record and say that my answer was just as correct as the ones with the fancy explainations! I mean, why can't a girl get props when she was the first one with the correct answer! just sayin'!
Girl, I'm givin' you props. Good job!0 -
The resultant for must be in the third quadrant. If the 20 degree force is >> than the 80, then the force is at 200 degrees. If the 80 is >> than the 20 degree force, then the force is at 260 degrees. Either way, the combination of the forces will result with an equilibrium force in the third quadrant.0
-
It goes without saying that Changing__Christina gave the correct answer long before I did. Great job, Christina!0
-
^^^ This guy specializes in soil... ing himself.I bet you never thought a homeless hobo who smells of booze and cigarettes would discuss physics with you, huh?0 -
I FIGURED IT OUT!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
okay so i went and looked on a seperate physics website!!!
each quadrant contains 90 degrees.
you find the resultant by adding together the 2 angles (80 + 20)
therefore the resultant is 100
which lies in the 2nd quadrant
you find the equilibrium by adding 180 degrees to that (because its oppsite)
this equals 280, which lies in the 4th quadrant.
thank god for other professors,
and thank you all for helping me!0 -
 0
0 -
Can someone please go on the record and say that my answer was just as correct as the ones with the fancy explainations! I mean, why can't a girl get props when she was the first one with the correct answer! just sayin'!
Girl, I'm givin' you props. Good job!
Finally!!!! I've been trying for an hour to get credit! Copy cats!0 -
It goes without saying that Changing__Christina gave the correct answer long before I did. Great job, Christina!
Thank you sooo much! I would like to thank my fans! 0
0 -

Soooo the resultant force is in the first quadrant.....equal and opposite of that would be the third quadrant....not the fourth.0 -
****.0
-
I FIGURED IT OUT!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
okay so i went and looked on a seperate physics website!!!
each quadrant contains 90 degrees.
you find the resultant by adding together the 2 angles (80 + 20)
therefore the resultant is 100
which lies in the 2nd quadrant
you find the equilibrium by adding 180 degrees to that (because its oppsite)
this equals 280, which lies in the 4th quadrant.
thank god for other professors,
and thank you all for helping me!
I don't think this is correct. that isn't what C is! sorry that you were wrong! 0
sorry that you were wrong! 0 -
TO GET THE ANGLE I HAVE TO USE A PROTRACTOR...
god crammit.
this shouldnt be so difficult.
i now understand that the answer is in the 3rd quadrant.
but i'd like to get there you know? hahahahaa0 -
Seriously, why are you stressing this? What's the worst that could happen?
 0
0
This discussion has been closed.
Categories
- All Categories
- 1.4M Health, Wellness and Goals
- 398.1K Introduce Yourself
- 44.7K Getting Started
- 261K Health and Weight Loss
- 176.4K Food and Nutrition
- 47.7K Recipes
- 233K Fitness and Exercise
- 462 Sleep, Mindfulness and Overall Wellness
- 6.5K Goal: Maintaining Weight
- 8.7K Goal: Gaining Weight and Body Building
- 153.5K Motivation and Support
- 8.4K Challenges
- 1.4K Debate Club
- 96.5K Chit-Chat
- 2.6K Fun and Games
- 4.8K MyFitnessPal Information
- 12 News and Announcements
- 21 MyFitnessPal Academy
- 1.5K Feature Suggestions and Ideas
- 3.2K MyFitnessPal Tech Support Questions





