Why fast food makes you fat

_Waffle_
Posts: 13,049 Member
I've been thinking quite a bit about how simple this diet and losing weight thing really is. We're all here on MFP for many reasons but using the app comes down to simply counting calories. Is it really this simple? We just figure out how many calories we need a day and then we subtract that from the calories we eat. If the number is a negative we should lose weight.
Then I was thinking about the calories I eat. Why do I eat these? For energy of course. I need this food for energy that I used during the day. Calories are simply energy. So what does energy have to do with my weight? Do you remember Einstein's Theory of General Relativity?
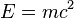
E is energy, m is mass, and c is the speed of light. I'm not the best with math but it's really obvious that if we subtract energy from one side then we'll have to lose mass on the other side. It's just that simple. Less energy = less mass on my body.
There was however one small thing that kept bugging me about this. Do I need to worry about the speed of light part of this equation. Initially I thought it didn't matter because we're not catching food at the speed of light. If we did it would result in a huge increase of mass when we stopped it.
That's when it all clicked in my head. Fast food!

Whenever we run out and grab fast food the extra energy from the speed of the fast food is transferred to us and results in us having more mass. Remember, energy = mass. Since the food isn't moving at the speed of light it doesn't make an instant difference but the little bit of extra speed we get from fast food will result in you obtaining more calories than you thought.
I haven't worked out an actual formula yet but I plan on testing this out. I'll eat fast food for a couple of weeks and see how many extra pounds I gain if I keep the calories the same. That should give me an idea of what % of calories I need to add to fast food items to get the real amount of energy that it gives us. This could be slightly offset if we grab the fast food in a car through the drive thru. I'll have to split this up and see if that makes a difference and I might test this out with delivery pizza since the drivers often speed to bring it to you.
Back when people used to take horses or walk to a store to get food we were all slimmer and more healthy. A slower lifestyle seems to have a very real effect on the amount of energy you intake. Perhaps this should be considered with microwaveable meals too? The atoms in the food are excited by the microwave and that means extra energy for your body when you eat it. I'm pretty sure that the fast food industry knows about this effect and they're trying to hide the fact that you obtain more energy than the listed calories when you eat fast food.
Then I was thinking about the calories I eat. Why do I eat these? For energy of course. I need this food for energy that I used during the day. Calories are simply energy. So what does energy have to do with my weight? Do you remember Einstein's Theory of General Relativity?
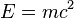
E is energy, m is mass, and c is the speed of light. I'm not the best with math but it's really obvious that if we subtract energy from one side then we'll have to lose mass on the other side. It's just that simple. Less energy = less mass on my body.
There was however one small thing that kept bugging me about this. Do I need to worry about the speed of light part of this equation. Initially I thought it didn't matter because we're not catching food at the speed of light. If we did it would result in a huge increase of mass when we stopped it.
That's when it all clicked in my head. Fast food!

Whenever we run out and grab fast food the extra energy from the speed of the fast food is transferred to us and results in us having more mass. Remember, energy = mass. Since the food isn't moving at the speed of light it doesn't make an instant difference but the little bit of extra speed we get from fast food will result in you obtaining more calories than you thought.
I haven't worked out an actual formula yet but I plan on testing this out. I'll eat fast food for a couple of weeks and see how many extra pounds I gain if I keep the calories the same. That should give me an idea of what % of calories I need to add to fast food items to get the real amount of energy that it gives us. This could be slightly offset if we grab the fast food in a car through the drive thru. I'll have to split this up and see if that makes a difference and I might test this out with delivery pizza since the drivers often speed to bring it to you.
Back when people used to take horses or walk to a store to get food we were all slimmer and more healthy. A slower lifestyle seems to have a very real effect on the amount of energy you intake. Perhaps this should be considered with microwaveable meals too? The atoms in the food are excited by the microwave and that means extra energy for your body when you eat it. I'm pretty sure that the fast food industry knows about this effect and they're trying to hide the fact that you obtain more energy than the listed calories when you eat fast food.
0
Replies
-
 0
0 -
:drinker:0
-
I enjoyed this! I love humor, intelligently done.0
-
 0
0 -
Back when people used to take horses or walk to a store to get food we were all slimmer and more healthy. A slower lifestyle seems to have a very real effect on the amount of energy you intake.
Love this part.0 -
LOL0
-

How YOU doin'??? LOVIN' that profile pic! 0
0 -

How YOU doin'??? LOVIN' that profile pic!
I like you.0 -
I think I need to keep you busy..see what happens when you have alot of time...0
-

LOL!
OP, I love you. :drinker:0 -
Thank you for this great post. I have been trying to figure out why fast food always makes me fatter than eating clean, and this shows a really good explanation. You are obviously a very smart guy.0
-
Thank you for this great post. I have been trying to figure out why fast food always makes me fatter than eating clean, and this shows a really good explanation. You are obviously a very smart guy.
QUICK! Get in the van, I have candy and you're purty :flowerforyou:0 -
This is why I never eat in-flight meals!
 0
0 -
this is actually incorrect, and I think I know why you are confused
E=mc2 is not the whole story, it only applies to mass that is not moving
FAST food is obviously moving so..
E^2=(MC^2)^2 +(PC)^2
This way you can account for momentum0 -
lmao :drinker:0
-

...my god. What has science done?!0 -
Brilliant!0
-
I cannot believe I didn't realize this already. You, sir, have changed my life.
:flowerforyou:0 -
This made me feel a funny.
And want a Big Mac.0 -
I'm craving some fries.... Mmmmmmm0
-
E^2=(MC^2)^2 +(PC)^2
This way you can account for momentum
This could be made simpler in practice. We need to find the instantaneous rate of additional energy/weight gained by taking the first derivative of your equation.
f(E)= ((mc^2)^2+((pc)^2)/(E^2))
f ' (E) = (2 ( (mc^2+pcE^2) - (E(mc^2)^2 + ((pc^2) / 2) / E^4)
So for any given food and momentum we should be able to find the precise rate of weight gain.0 -
This post makes me sad that you aren't on my friend list anymore
 0
0 -

How YOU doin'??? LOVIN' that profile pic!
Oh my, that IS a nice profile pic...0 -
I wonder if it makes a difference how fast you eat the food. Usually my food disappears at twice the speed of light.0
-
 0
0 -
But, what if the service is really really slow. Like I woulda gotten it faster if I woulda jumped the counter and made it myself. Cuz this one time it took them over a half an hour to make an order and if I wasn't in the middle of a food desert I woulda left and gotten food somewhere else.0
This discussion has been closed.
Categories
- All Categories
- 1.4M Health, Wellness and Goals
- 398.1K Introduce Yourself
- 44.7K Getting Started
- 261K Health and Weight Loss
- 176.4K Food and Nutrition
- 47.7K Recipes
- 233K Fitness and Exercise
- 462 Sleep, Mindfulness and Overall Wellness
- 6.5K Goal: Maintaining Weight
- 8.7K Goal: Gaining Weight and Body Building
- 153.5K Motivation and Support
- 8.4K Challenges
- 1.4K Debate Club
- 96.5K Chit-Chat
- 2.6K Fun and Games
- 4.8K MyFitnessPal Information
- 12 News and Announcements
- 21 MyFitnessPal Academy
- 1.5K Feature Suggestions and Ideas
- 3.2K MyFitnessPal Tech Support Questions



















